Custom vectorization¶
Contents
Introduction¶
One of the strengths of NumPy is that it can be used to build new objects or to subclass the ndarray object. This later process is a bit tedious but it is worth the effort because it allows you to improve the ndarray object to suit your problem. We’ll examine in the following section two real-world cases (typed list and memory-aware array) that are extensively used in the glumpy project (that I maintain) while the last one (double precision array) is a more academic case.
Typed list¶
Typed list (also known as ragged array) is a list of items that all have the same data type (in the sense of NumPy). They offer both the list and the ndarray API (with some restriction of course) but because their respective APIs may not be compatible in some cases, we have to make choices. For example, concerning the + operator, we’ll choose to use the NumPy API where the value is added to each individual item instead of expanding the list by appending a new item (1).
>>> l = TypedList([[1,2], [3]])
>>> print(l)
[1, 2], [3]
>>> print(l+1)
[2, 3], [4]
From the list API, we want our new object to offer the possibility of inserting, appending and removing items seamlessly.
Creation¶
Since the object is dynamic by definition, it is important to offer a general-purpose creation method powerful enough to avoid having to do later manipulations. Such manipulations, for example insertion/deletion, cost a lot of operations and we want to avoid them. Here is a proposal (among others) for the creation of a TypedList object.
def __init__(self, data=None, sizes=None, dtype=float)
"""
Parameters
----------
data : array_like
An array, any object exposing the array interface, an object
whose __array__ method returns an array, or any (nested) sequence.
sizes: int or 1-D array
If `itemsize` is an integer, N, the array will be divided
into elements of size N. If such partition is not possible,
an error is raised.
If `itemsize` is a 1-D array, the array will be divided into
elements whose successive sizes will be picked from itemsize.
If the sum of itemsize values is different from array size,
an error is raised.
dtype: np.dtype
Any object that can be interpreted as a NumPy data type.
"""
This API allows creating an empty list or creating a list from some external data. Note that in the latter case, we need to specify how to partition the data into several items or they will split into 1-size items. It can be a regular partition (i.e. each item is 2 data long) or a custom one (i.e. data must be split in items of size 1, 2, 3 and 4 items).
>>> L = TypedList([[0], [1,2], [3,4,5], [6,7,8,9]])
>>> print(L)
[ [0] [1 2] [3 4 5] [6 7 8] ]
>>> L = TypedList(np.arange(10), [1,2,3,4])
[ [0] [1 2] [3 4 5] [6 7 8] ]
At this point, the question is whether to subclass the ndarray class or to use an internal ndarray to store our data. In our specific case, it does not really make sense to subclass ndarray because we don’t really want to offer the ndarray interface. Instead, we’ll use an ndarray for storing the list data and this design choice will offer us more flexibility.
╌╌╌╌┬───┐┌───┬───┐┌───┬───┬───┐┌───┬───┬───┬───┬╌╌╌╌╌
│ 0 ││ 1 │ 2 ││ 3 │ 4 │ 5 ││ 6 │ 7 │ 8 │ 9 │
╌╌╌┴───┘└───┴───┘└───┴───┴───┘└───┴───┴───┴───┴╌╌╌╌╌╌
item 1 item 2 item 3 item 4
To store the limit of each item, we’ll use an items array that will take care of storing the position (start and end) for each item. For the creation of a list, there are two distinct cases: no data is given or some data is given. The first case is easy and requires only the creation of the _data and _items arrays. Note that their size is not null since it would be too costly to resize the array each time we insert a new item. Instead, it’s better to reserve some space.
First case. No data has been given, only dtype.
self._data = np.zeros(512, dtype=dtype)
self._items = np.zeros((64,2), dtype=int)
self._size = 0
self._count = 0
Second case. Some data has been given as well as a list of item sizes (for other cases, see full code below)
self._data = np.array(data, copy=False)
self._size = data.size
self._count = len(sizes)
indices = sizes.cumsum()
self._items = np.zeros((len(sizes),2),int)
self._items[1:,0] += indices[:-1]
self._items[0:,1] += indices
Access¶
Once this is done, every list method requires only a bit of computation and playing with the different key when getting, inserting or setting an item. Here is the code for the __getitem__ method. No real difficulty but the possible negative step:
def __getitem__(self, key):
if type(key) is int:
if key < 0:
key += len(self)
if key < 0 or key >= len(self):
raise IndexError("Tuple index out of range")
dstart = self._items[key][0]
dstop = self._items[key][1]
return self._data[dstart:dstop]
elif type(key) is slice:
istart, istop, step = key.indices(len(self))
if istart > istop:
istart,istop = istop,istart
dstart = self._items[istart][0]
if istart == istop:
dstop = dstart
else:
dstop = self._items[istop-1][1]
return self._data[dstart:dstop]
elif isinstance(key,str):
return self._data[key][:self._size]
elif key is Ellipsis:
return self.data
else:
raise TypeError("List indices must be integers")
Exercise¶
Modification of the list is a bit more complicated, because it requires managing memory properly. Since it poses no real difficulty, we left this as an exercise for the reader. For the lazy, you can have a look at the code below. Be careful with negative steps, key range and array expansion. When the underlying array needs to be expanded, it’s better to expand it more than necessary in order to avoid future expansion.
setitem
L = TypedList([[0,0], [1,1], [0,0]])
L[1] = 1,1,1
╌╌╌╌┬───┬───┐┌───┬───┐┌───┬───┬╌╌╌╌╌
│ 0 │ 0 ││ 1 │ 1 ││ 2 │ 2 │
╌╌╌┴───┴───┘└───┴───┘└───┴───┴╌╌╌╌╌╌
item 1 item 2 item 3
╌╌╌╌┬───┬───┐┌───┬───┲━━━┓┌───┬───┬╌╌╌╌╌
│ 0 │ 0 ││ 1 │ 1 ┃ 1 ┃│ 2 │ 2 │
╌╌╌┴───┴───┘└───┴───┺━━━┛└───┴───┴╌╌╌╌╌╌
item 1 item 2 item 3
delitem
L = TypedList([[0,0], [1,1], [0,0]])
del L[1]
╌╌╌╌┬───┬───┐┏━━━┳━━━┓┌───┬───┬╌╌╌╌╌
│ 0 │ 0 │┃ 1 ┃ 1 ┃│ 2 │ 2 │
╌╌╌┴───┴───┘┗━━━┻━━━┛└───┴───┴╌╌╌╌╌╌
item 1 item 2 item 3
╌╌╌╌┬───┬───┐┌───┬───┬╌╌╌╌╌
│ 0 │ 0 ││ 2 │ 2 │
╌╌╌┴───┴───┘└───┴───┴╌╌╌╌╌╌
item 1 item 2
insert
L = TypedList([[0,0], [1,1], [0,0]])
L.insert(1, [3,3])
╌╌╌╌┬───┬───┐┌───┬───┐┌───┬───┬╌╌╌╌╌
│ 0 │ 0 ││ 1 │ 1 ││ 2 │ 2 │
╌╌╌┴───┴───┘└───┴───┘└───┴───┴╌╌╌╌╌╌
item 1 item 2 item 3
╌╌╌╌┬───┬───┐┏━━━┳━━━┓┌───┬───┐┌───┬───┬╌╌╌╌╌
│ 0 │ 0 │┃ 3 ┃ 3 ┃│ 1 │ 1 ││ 2 │ 2 │
╌╌╌┴───┴───┘┗━━━┻━━━┛└───┴───┘└───┴───┴╌╌╌╌╌╌
item 1 item 2 item 3 item 4
Sources¶
array_list.py (solution to the exercise)
Memory aware array¶
Glumpy¶
Glumpy is an OpenGL-based interactive visualization library in Python whose goal is to make it easy to create fast, scalable, beautiful, interactive and dynamic visualizations.
Figure 6.1
Simulation of a spiral galaxy using the density wave theory.

Figure 6.2
Tiger display using collections and 2 GL calls

Glumpy is based on a tight and seamless integration with NumPy arrays. This means you can manipulate GPU data as you would with regular NumPy arrays and glumpy will take care of the rest. But an example is worth a thousand words:
from glumpy import gloo
dtype = [("position", np.float32, 2), # x,y
("color", np.float32, 3)] # r,g,b
V = np.zeros((3,3),dtype).view(gloo.VertexBuffer)
V["position"][0,0] = 0.0, 0.0
V["position"][1,1] = 0.0, 0.0
V is a VertexBuffer which is both a GPUData and a NumPy array. When V is modified, glumpy takes care of computing the smallest contiguous block of dirty memory since it was last uploaded to GPU memory. When this buffer is to be used on the GPU, glumpy takes care of uploading the “dirty” area at the very last moment. This means that if you never use V, nothing will be ever uploaded to the GPU! In the case above, the last computed “dirty” area is made of 88 bytes starting at offset 0 as illustrated below:
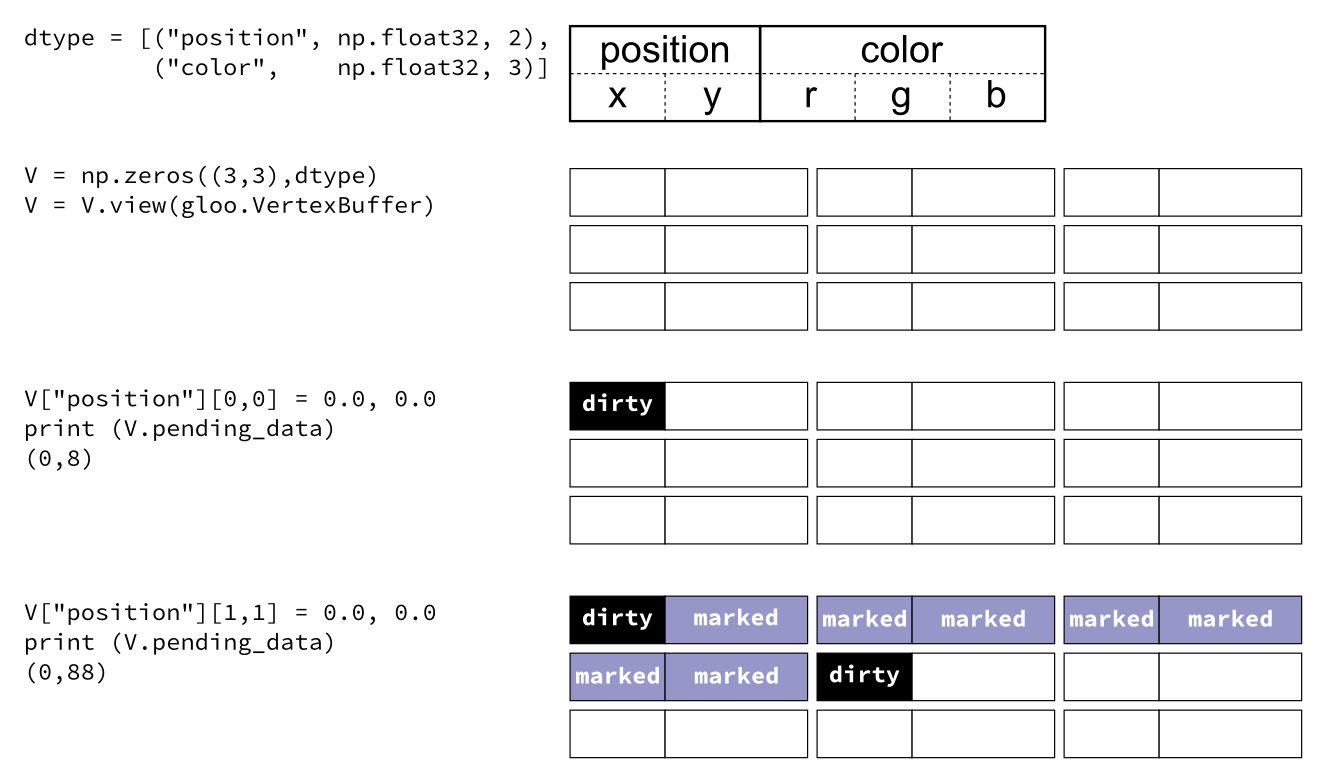
Note
When a buffer is created, it is marked as totally dirty, but for the sake of illustration, just pretend this is not the case here.
Glumpy will thus end up uploading 88 bytes while only 16 bytes have been actually modified. You might wonder if this optimal. Actually, most of the time it is, because uploading some data to a buffer requires a lot of operations on the GL side and each call has a fixed cost.
Array subclass¶
As explained in the Subclassing ndarray documentation, subclassing ndarray is complicated by the fact that new instances of ndarray classes can come about in three different ways:
Explicit constructor call
View casting
New from template
However our case is simpler because we’re only interested in the view casting. We thus only need to define the __new__ method that will be called at each instance creation. As such, the GPUData class will be equipped with two properties:
extents: This represents the full extent of the view relatively to the base array. It is stored as a byte offset and a byte size.
pending_data: This represents the contiguous dirty area as (byte offset, byte size) relatively to the extents property.
class GPUData(np.ndarray):
def __new__(cls, *args, **kwargs):
return np.ndarray.__new__(cls, *args, **kwargs)
def __init__(self, *args, **kwargs):
pass
def __array_finalize__(self, obj):
if not isinstance(obj, GPUData):
self._extents = 0, self.size*self.itemsize
self.__class__.__init__(self)
self._pending_data = self._extents
else:
self._extents = obj._extents
Computing extents¶
Each time a partial view of the array is requested, we need to compute the extents of this partial view while we have access to the base array.
def __getitem__(self, key):
Z = np.ndarray.__getitem__(self, key)
if not hasattr(Z,'shape') or Z.shape == ():
return Z
Z._extents = self._compute_extents(Z)
return Z
def _compute_extents(self, Z):
if self.base is not None:
base = self.base.__array_interface__['data'][0]
view = Z.__array_interface__['data'][0]
offset = view - base
shape = np.array(Z.shape) - 1
strides = np.array(Z.strides)
size = (shape*strides).sum() + Z.itemsize
return offset, offset+size
else:
return 0, self.size*self.itemsize
Keeping track of pending data¶
One extra difficulty is that we don’t want all the views to keep track of the dirty area but only the base array. This is the reason why we don’t instantiate the self._pending_data in the second case of the __array_finalize__ method. This will be handled when we need to update some data as during a __setitem__ call for example:
def __setitem__(self, key, value):
Z = np.ndarray.__getitem__(self, key)
if Z.shape == ():
key = np.mod(np.array(key)+self.shape, self.shape)
offset = self._extents[0]+(key * self.strides).sum()
size = Z.itemsize
self._add_pending_data(offset, offset+size)
key = tuple(key)
else:
Z._extents = self._compute_extents(Z)
self._add_pending_data(Z._extents[0], Z._extents[1])
np.ndarray.__setitem__(self, key, value)
def _add_pending_data(self, start, stop):
base = self.base
if isinstance(base, GPUData):
base._add_pending_data(start, stop)
else:
if self._pending_data is None:
self._pending_data = start, stop
else:
start = min(self._pending_data[0], start)
stop = max(self._pending_data[1], stop)
self._pending_data = start, stop
Conclusion¶
As explained on the NumPy website, NumPy is the fundamental package for scientific computing with Python. However, as illustrated in this chapter, the usage of NumPy strengths goes far beyond a mere multi-dimensional container of generic data. Using ndarray as a private property in one case (TypedList) or directly subclassing the ndarray class (GPUData) to keep track of memory in another case, we’ve seen how it is possible to extend NumPy’s capabilities to suit very specific needs. The limit is only your imagination and your experience.
